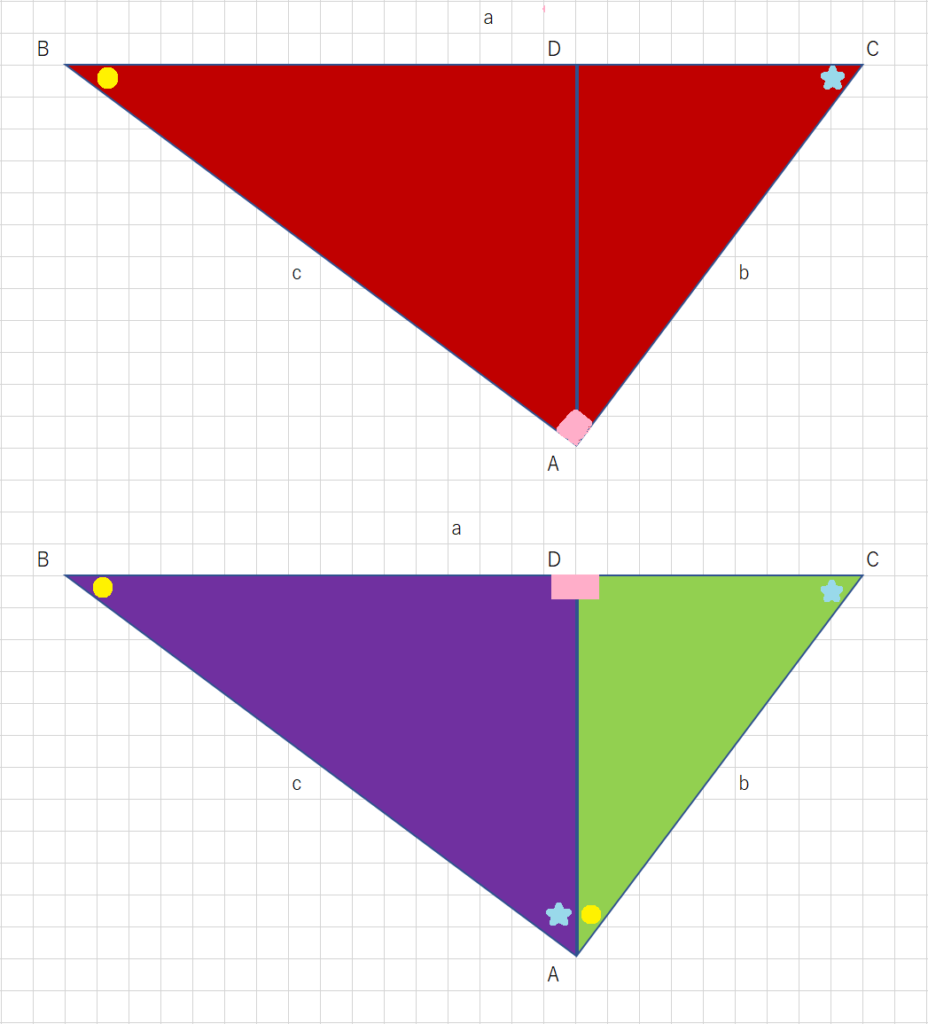
して,三角形が直角三角 形であるかどうかを判 断することができる. ・三平方の定理を利用し て,正方形の対角線や正 三角形の高さなどを求 めることができる. ・特別な直角三角形の3 辺 の比を使って,直角三角 形の辺の長さを求める ことができる.直角二等辺三角形と三平方の定理と計算、例題 例題として、下図に直角二等辺三角形の辺の長さを三平方の定理を用いて計算しましょう。 三平方の定理より、底辺と高さの二乗和の平方根が斜辺の長さになります。よって、 です。三平方の定理の証明 AB=c, BC=a, AC=b, ∠ACB=90°の直角三角形ABCと合同な直角三角形を図のように並べて正方形ABDFをつくる。 正方形ABDFの面積をSとすると、1辺がcなので S=c2 ① また、正方形ABDFは△ABCと合同な三角形4つと正方形EGHCでできている。
Python 三平方の定理 Unpyside
3平方の定理 直角三角形
3平方の定理 直角三角形- 3平方 の定理で、直角二等辺三角形になるときは1対1対ルート2 ですが、それを利用して解く問題がわかりません。斜辺が4 センチの直角二等辺三角形では、残りの長さは何センチになりますか。わ かりやすい解説お願いします! 3 1、勾股定理 直角三角形的两条直角边的平方和等于斜边的平方。 也叫毕达哥拉斯定理。 表达式为a b =c 。 勾股定理 2、射影定理 在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的




直角三角形 Twitter Search
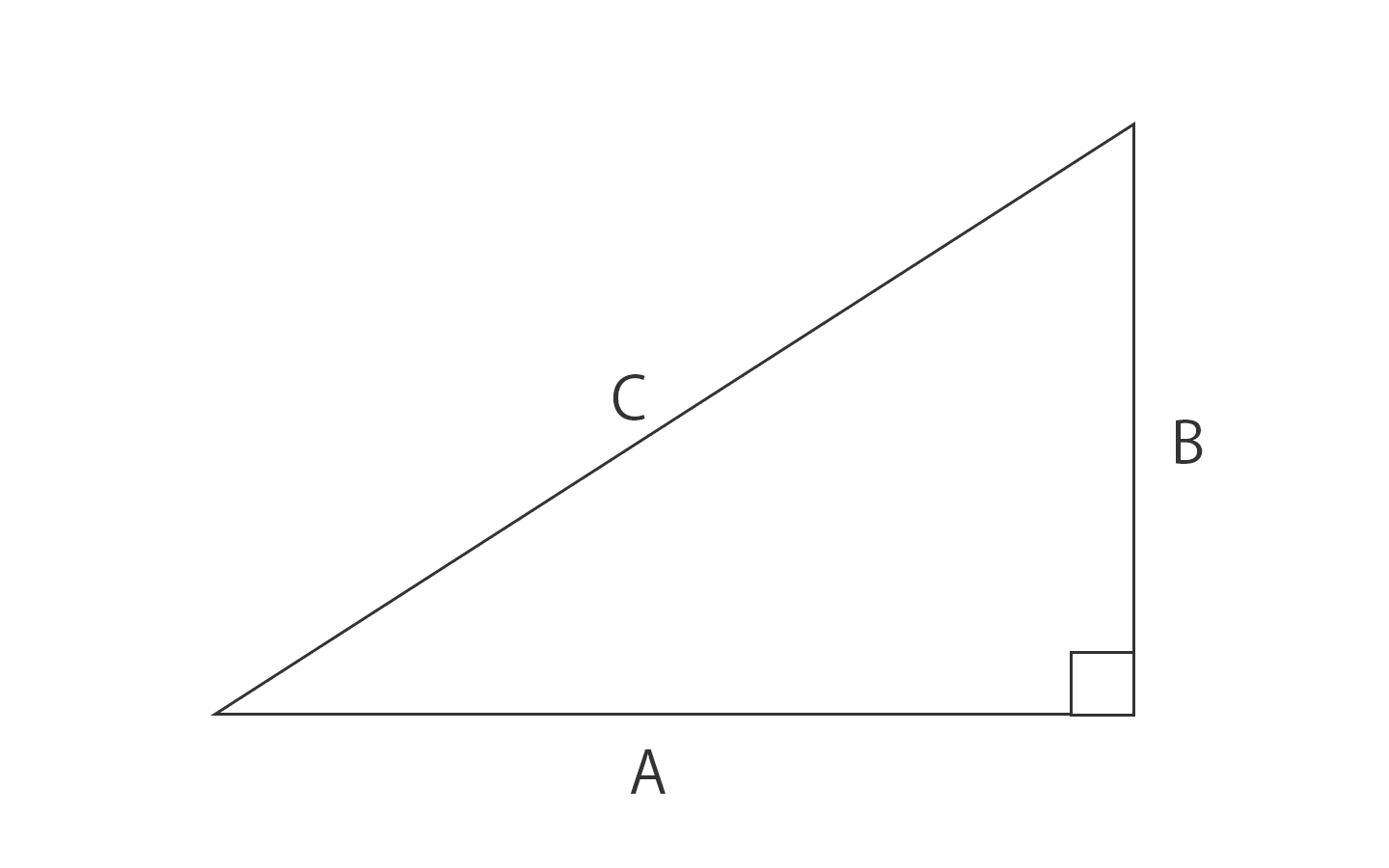
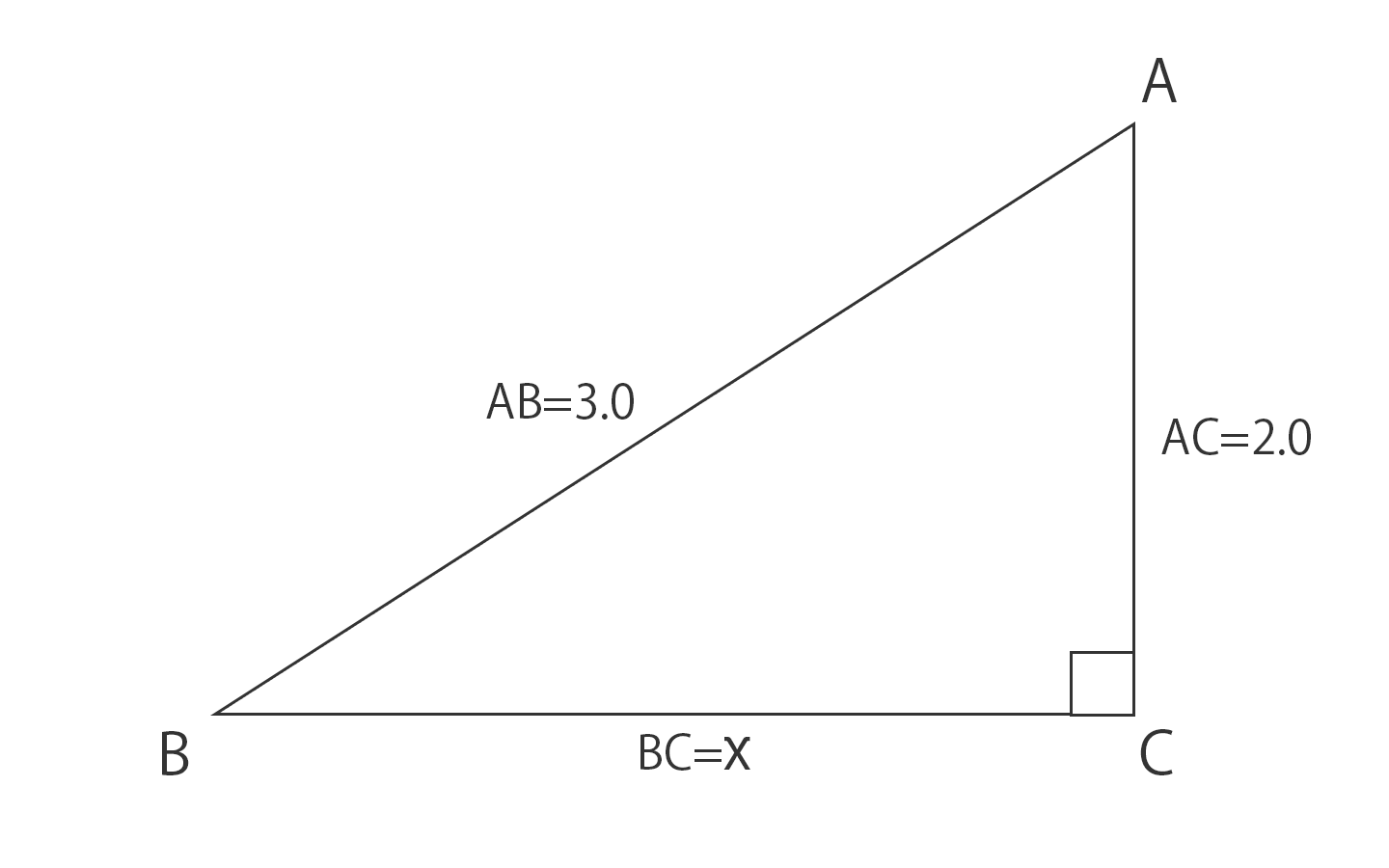
次のような直角三角形の3辺の長さについては, a 2 b 2 =c 2 が成り立ちます.(これを 三平方の定理 といいます.)頂点Aから垂線をおろして直角三角形をつくる。 三平方の定理に当てはめる。 x 2 1 2 =3 2 x 2 =91 x 2 =8 x=±2 2 x>0よりx=2 2 答 2 2 cm 確認次のそれぞれの三角形で、頂点Aから辺BCにおろした垂線の長さを求めよ。 答表示 1辺8cmの正三角形 A B C 4 3 cm AB=AC=29cm, BC=40cm直角三角形における3辺の長さによる定理を 三平方の定理 (さんへいほうのていり)と言います。ピタゴラスの定理とも言われます。 三平方の定理では、直角三角形の斜辺をc、その他の辺をそれぞれa、bとした場合に、 a 2 b 2 = c 2 が成り立ちます。
3辺のうち、「a 2 +b 2 =c 2 」の 「c」 になる可能性があるのは、 1番長い5cm の辺だけだよ。 つまり、3 2 +4 2 が5 2 と等しくなるかどうか調べればいいね。 等しいならば、直角三角形だ。三平方の定理とは、古代ギリシアの数学者である「ピタゴラス」の名前を取って、「ピタゴラスの定理」と呼ぶこともある定理で、「直角三角形の3辺の長さの関係」表す定理です。 直角三角形とは、中学数学で散々見てきた これですね。 2辺が直角 (すなわち90°)となるように接し、その2辺の端を繋ぐ斜めの線を付けることで完成するこの図形、この長さの関係は実 それは3平方の定理ではなく 余弦定理といいます ABCに対して BC^2=AB^2AC^22ABACcos∠BAC が成り立つ ∠BAC=90°の時 ABCは直角三角形となり cos∠BAC=0となり 3平方の定理
直角三角形性质 直角三角形是一个几何图形,是有一个角为直角的三角形,有普通的直角三角形和等腰直角三角形两种。特殊性质有: 1、勾股定理,直角三角形两直角边的平方和等于斜边的平方。 2、在直角三角形中,两个锐角互余。直角三角形 110 /2件 表示件数 5 10 30 50 100 0 1 1245 60歳以上 / その他 / 非常に役に立った /平方 平方是一數乘以自己,以下以 5 2 為例說明: 直角三角形



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者
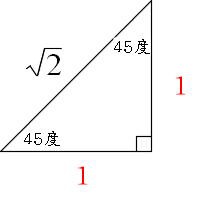
四平方の定理三平方の定理というと, 直角三角形において,(斜辺の2乗) = (他の2辺の2乗の和)が成り立つという有名な定理ですここでは, 三平方の定理(平面上の定理)を3次元に拡張した, 四平方の定理を紹介します 定理 3つの面が直角三角形で, 1つの頂点に直角が集まっている三角錐を考え左の直角三角形が正三角形を半分にしたものです。 3 3 辺の比は暗記で、 21√3 2 1 3 です。 次に、右の直角三角形に三平方の定理を使うと、 最後の 1 1 辺の長さが求まります。 最後の 1 1 辺の長さを y y とすると y2 =102 y 2 8 2 = 10 2 y2 64 = 100 y 2 64三平方の定理 (さんへいほうのていり)、 勾股弦の定理 (こうこげんのていり)とも呼ばれる。 ピタゴラスの定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残りの1辺の長さを知ることができる。




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学




三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト
三平方の定理 基本公式まとめ お疲れ様でした! これで三平方の定理の基本は バッチリです。 三平方の定理とは 直角三角形の長さを求めることができる便利な定理です。 そして、直角三角形の中には 特別な存在の三角形があります。 これらの直角三平方の定理の逆とは、三角形の3辺がa² b² = c² を満たせば、その三角形は直角三角形であるというものです。図形の証明問題などに使われる場合があるので、覚えておきましょう。 三平方の定理の 所属频道: 北师大版八年级数学上册 更新时间: 素材版本:PowerPoint03及以上版本 (ppt) 下载类型:免费下载 文件大小:278 KB 显示比例:普屏43 附件类型:rar 目录: 详细介绍 下载地址 相关下载 下载帮助 标签: 勾股定理 能得到直角三角形吗



Python 三平方の定理 Unpyside




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導
畢氏定理 直角三角形,長股平方短股平方=斜邊平方,一般表達為: a 2 b 2 =c 2 面積公式 長方形面積=長×寬; 345の三角形が直角三角形である理由 各辺が345の三角形って こんな感じで、ピタゴラスの定理にあてはまるよね! ピタゴラスの定理は、 直角三角形の3辺の長さは斜辺2 = 底辺2 高さ2 斜 辺 2 = 底 辺 2 高 さ 2 になる つまり、ピタゴラスの定理に三平方の定理とは 直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思います




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
直角三角形の3辺の長さの関係を表したもの だよ その関係っていうのは、 斜辺2 = 底辺2 高さ2 斜 辺 2 = 底 辺 2 高 さ 2 だよ定理(a,b,c),(a0,b0,c0)をそれぞれ長さが整数の直角三角形とする。このとき長さ が整数の直角三角形(a 00,b00,c)でうえの二つの三角形と相似ではないものが作れる。 斜辺について着目したとき不正確な言い方をすれば、(相似ではないと仮定して直角二等辺三角形と三平方の定理の関係は?3分でわかる計算、公式、辺の比、例題 直角三角形の斜辺の求め方は?1分でわかる計算、斜辺と高さ、辺の長さの関係 傾斜の計算とは?1分でわかる意味、勾配の高さ、長さ、角度の計算 管理人おすすめ!




三平方の定理の証明と使い方




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
まとめ:直角三角形の比3つを使い倒せ! 中学数学でよく使う直角三角形の比は次の3つ。 30、60の直角三角形 45の直角三角形 3 4 5の直角三角形 これを覚えるだけで三平方の定理を使わなくてよくなるから、 だいぶラクになるね。 いきなり覚えるのは三平方の定理直角三角形の辺の長さを計算する4つの問題の 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 中3数学では、 三平方の定理(ピタゴラスの定理) を勉強してきたよな? 簡単に復習すると、 直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、 a²+ b² = c² が成り立つ ってやつだったな。 さあ、この定理を使いこなせるようになるんだぞ。 今回はそのための基礎トレーニングだ。



三平方の定理を直角三角形以外の三角形に使う時の公式ってどうなりますか Yahoo 知恵袋



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog
ピタゴラスの定理とは、古代ギリシアの数学者で哲学者のピタゴラスが立ち上げた団体が発見した数学の定理のこと。直角三角形をなす3辺のうち、2辺の長さを知ることができれば、残り1辺の長さを知ることができるというものです。 公式:a² b² = c²




Python 三平方の定理 Unpyside



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube
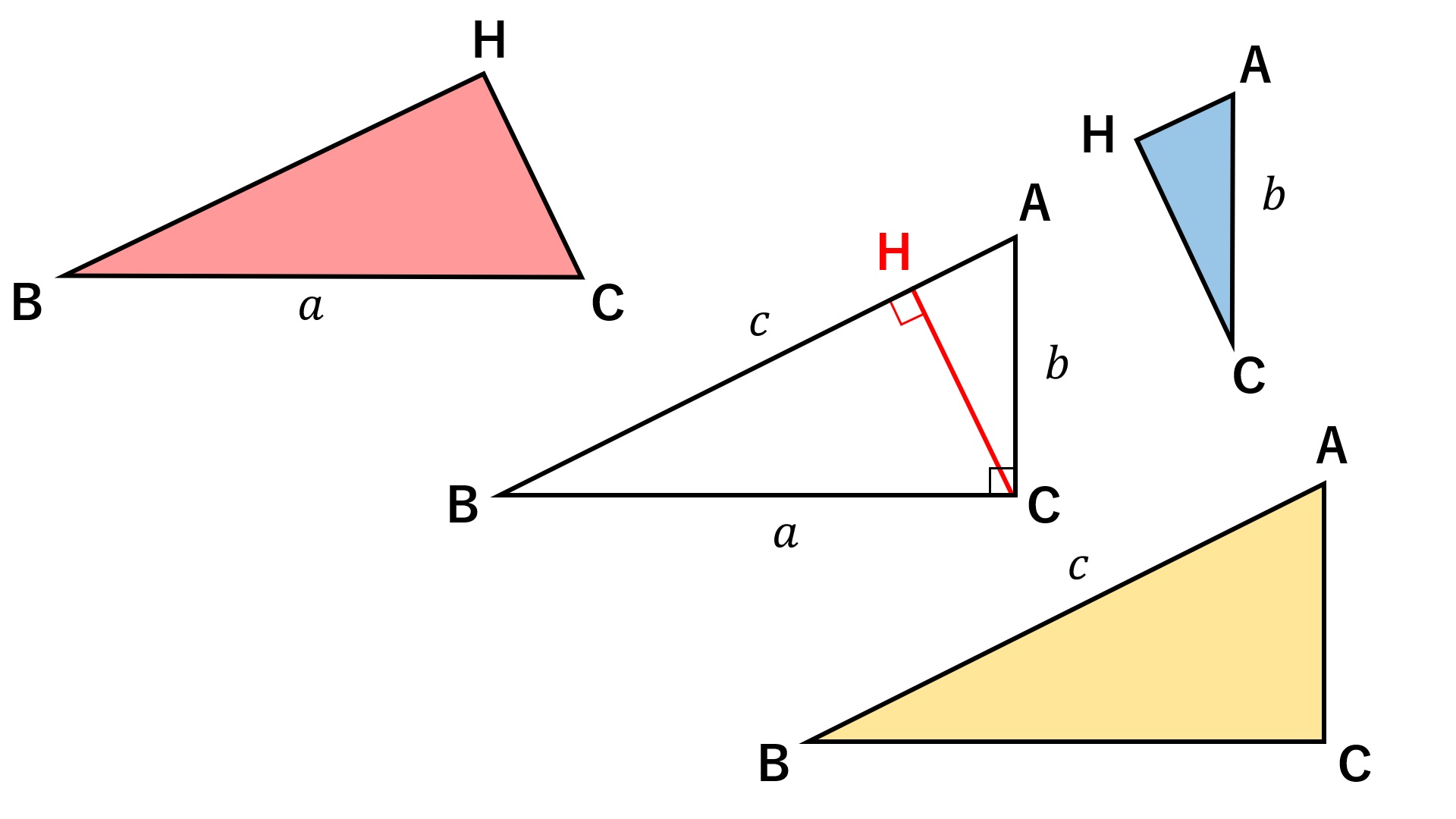



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




特別な直角三角形の辺の比 無料で使える中学学習プリント




三平方の定理について考える5 直角三角形の合同条件のひとつ 身勝手な主張



三平方の定理



Q Tbn And9gcsnbiv 7svsm 6o0qjqco66pmarde4rrmbqkrgwufvawvziomrf Usqp Cau




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座



質問にお答えします 小学生でもわかる数学とは 教育研究所arcs




三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも
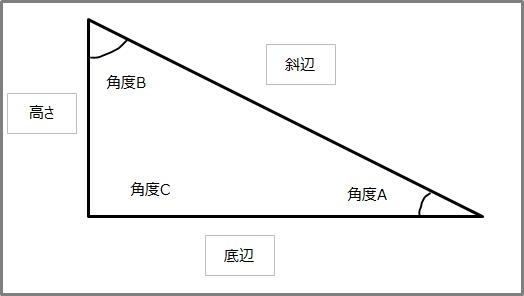



三平方の定理の計算 角度と長さ Nujonoa Blog




三平方の定理の証明と使い方



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド




直角三角形の辺の長さ 合同条件 面積について アタリマエ




三平方の定理 ピタゴラスの定理




直角三角形 Twitter Search




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




三平方の定理 自動計算サイト




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



1




三平方の定理の証明と使い方




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学
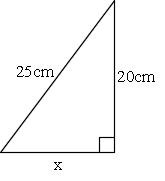



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




三平方の定理の応用




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理 特別な直角三角形 イ弋マ本ゼミナール
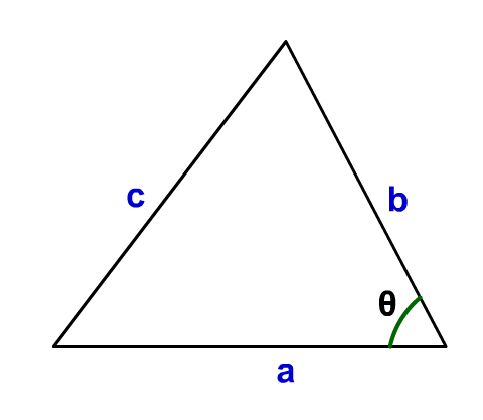



難しい 余弦定理 をシミュレーターを使って理解しよう 数学入門




三平方の定理 覚えておきたい基本公式を解説 数スタ




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




Catatan Tentang 中学数学 三平方の定理のキホン Junior Clear




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ
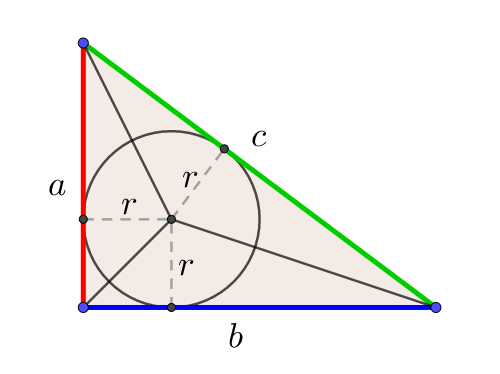



三平方の定理の証明4 直角三角形と内接円 キソカラ



三平方の定理 やややさしい数学




知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
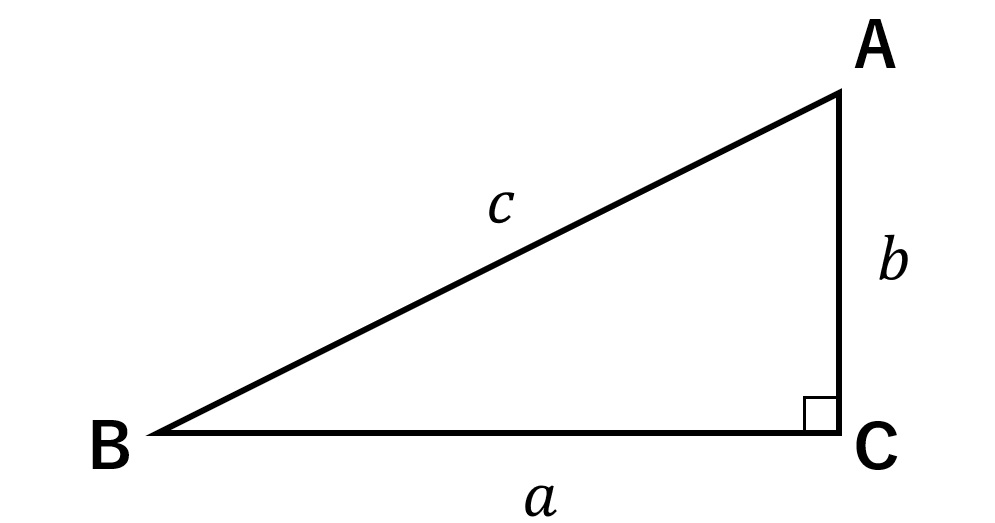



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方の定理で辺を求める Youtube




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者
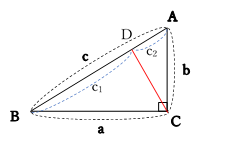



三平方の定理 おやじさん ネット




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
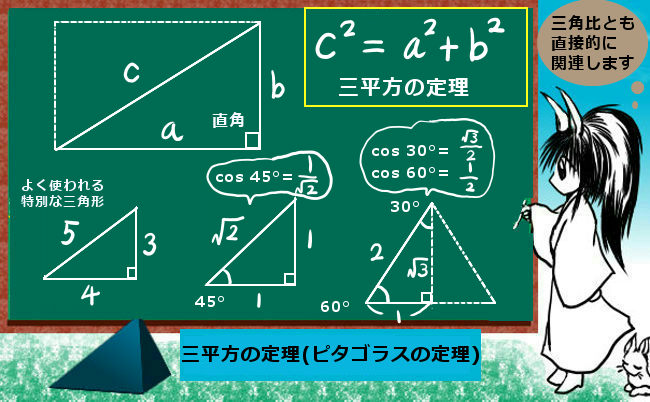



三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori



1




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
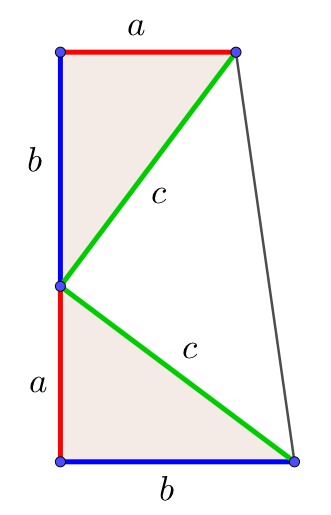



三平方の定理の証明3 大統領の台形 キソカラ



円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
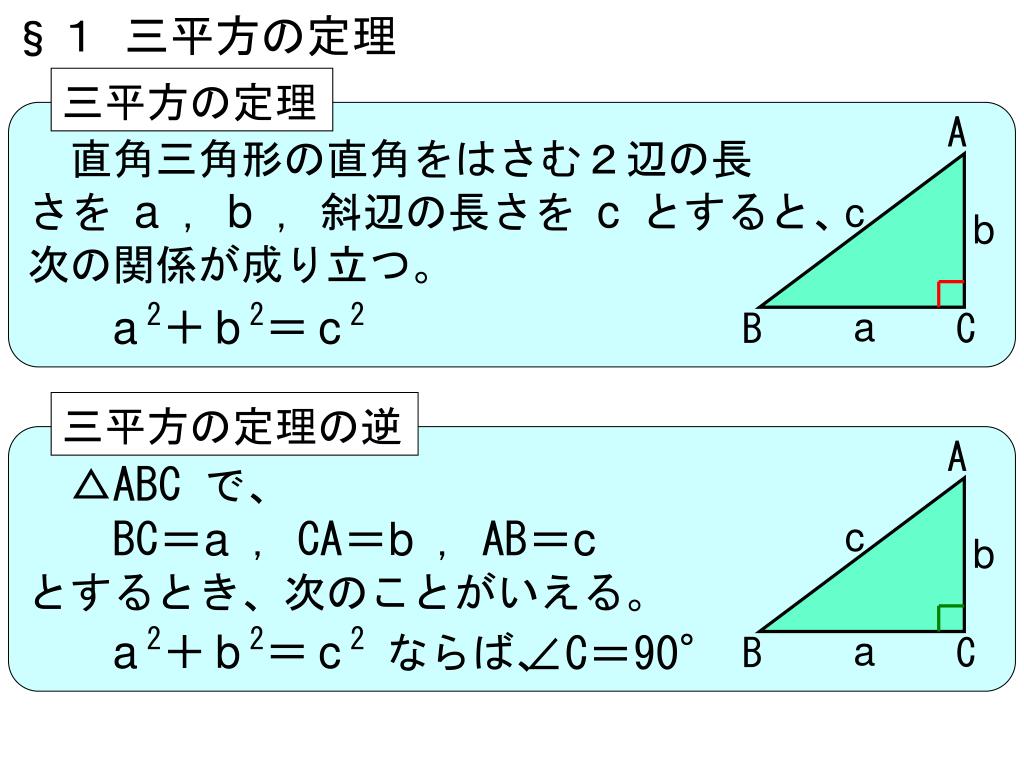



Ppt 6 三平方の定理 Powerpoint Presentation Free Download Id




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理の拡張について考えよう 理科好き子供の広場




三平方の定理を直角三角形二つで証明 Youtube




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
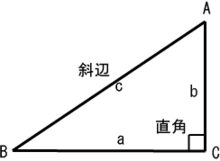



質問コーナー Discuss Scratch




数学 中3 61 三平方の定理 基本編 Youtube



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典
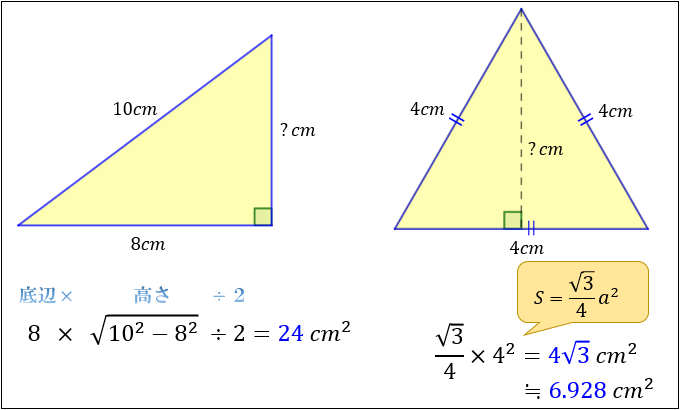



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora
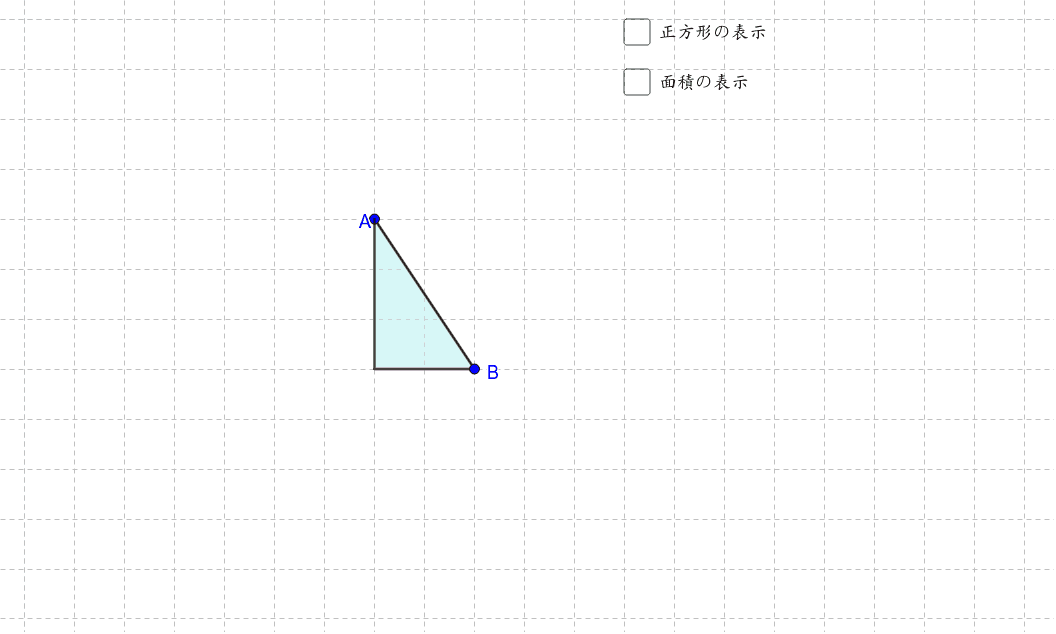



三平方の定理の導入 Geogebra




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




練習22がわかりません 三平方はわかりますがのこりのものがわかりません Clear



三角形の内角30度 60度 90度のとき辺の比は1 2 Root3になる Yahoo 知恵袋




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
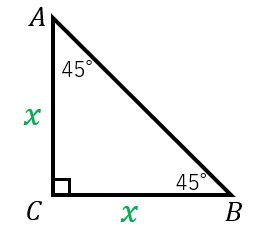



30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




無料 中3数学 基本解説 解答プリント 334 三平方の定理2 比の利用
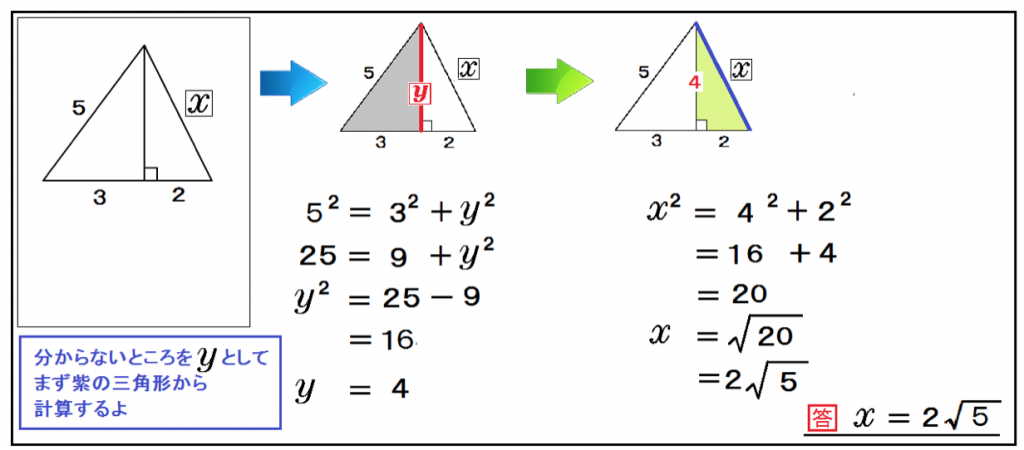



1 1 ルート2 三角形




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ



1
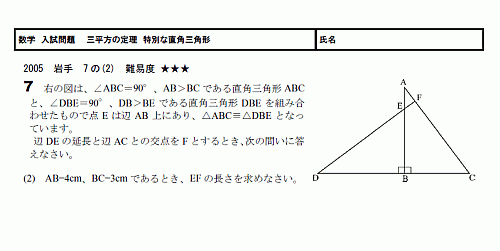



三平方の定理 スタディーx
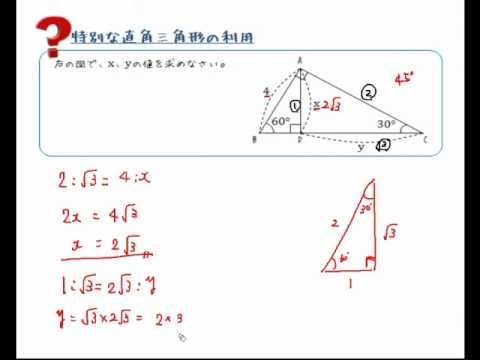



特別な直角三角形の利用 Youtube




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に
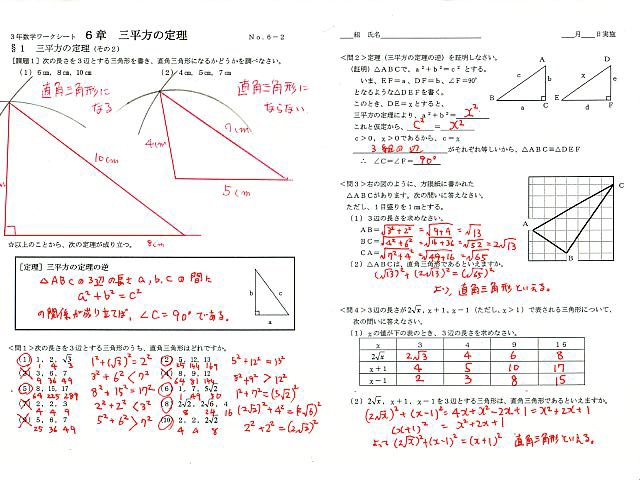



2 三平方の定理の逆 Mathweather4067のblog




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿